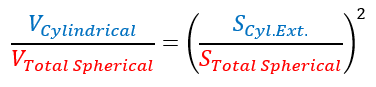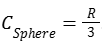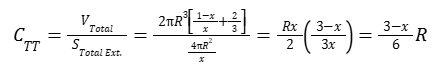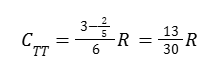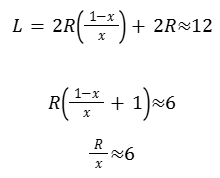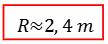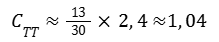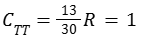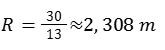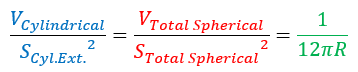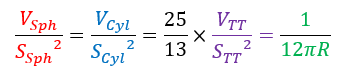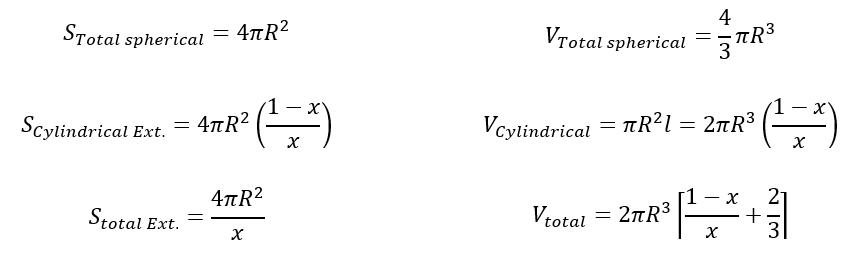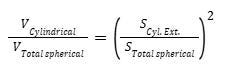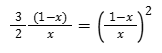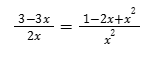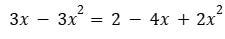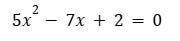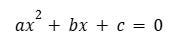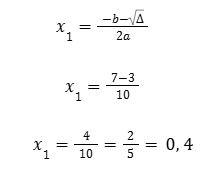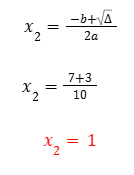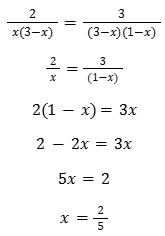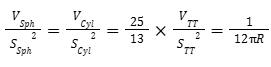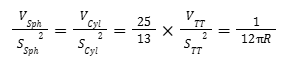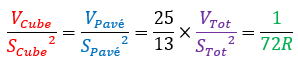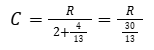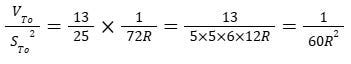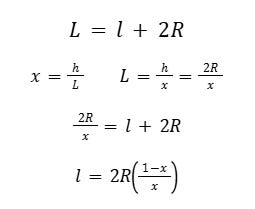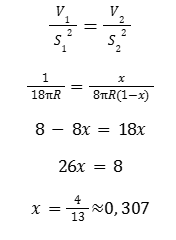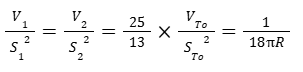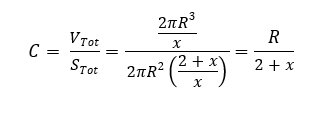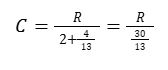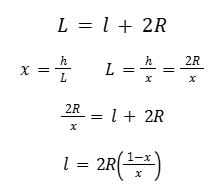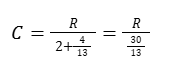Esclusivo/ G. Pierrez : La geometria nascosta del caso dell'UAP di Nimitz
L'ingegnere Guillaume Pierrez ha trovato un rapporto intrigante nelle proporzioni dell'UAP cosiddetto “TIC-TAC”.
Una forma che non tiene conto dell'aerodinamica
Durante una gara di Formula 1, sareste disposti a scommettere su un partecipante che si presenta con le ruote quadrate? Probabilmente no…
Tuttavia, questo è quasi il tipo di scommessa che i progettisti del TIC TAC (se esiste un progetto) avrebbero potuto fare.
Nell'ambito di un progetto di aeromobile supersonico, qualsiasi ingegnere aeronautico inizierebbe con una forma a punta di freccia. Questo è infatti ciò che la meccanica dei fluidi raccomanda per favorire il flusso d'aria e ridurre al minimo il riscaldamento della fusoliera.
È quindi del tutto impensabile di scegliere la forma di un TIC TAC per un aereomobile con questa capacità.
Anche se non conosciamo la sua tecnica di volo, sappiamo già una cosa essenziale:
la forma sembra prevalere sull'aerodinamica.
Il fenomeno è frutto di un progetto?
Prima di continuare, è opportuno confermare o confutare l'artificialità del fenomeno. Qualcuno giustamente obietterà che il comportamento descritto dai testimoni, la cinetica e molti altri aspetti non lasciano dubbi sulla natura artificiale del fenomeno.
È vero che tutti questi elementi costituiscono una serie di indizi molto forti.
Tuttavia, credo che sia possibile un approccio più tecnico e oggettivo.
Mi spiego utilizzando una lattina di soda:
Considerate la vostra lattina di alluminio. Pensate per un attimo a chi l'ha progettata e alla prima domanda che si è posto:
“Quali sono le dimensioni che garantiscono un volume ottimale con un costo minimo di alluminio? ”
Se consideriamo che una lattina è approssimativamente paragonabile a un cilindro, possiamo descrivere il suo volume e la sua superficie in base al suo raggio R e alla sua altezza h. Quindi stabilire una relazione tra volume, costo e superficie; senza entrare nei dettagli, la matematica ci permette di trovare la soluzione ideale.
Così facendo, il barattolo risultante porta letteralmente la “traccia matematica” della sua artificialità nelle sue dimensioni:
Immaginate ora un archeologo del futuro che trovi i resti della vostra lattina. Sarà in grado di misurare le dimensioni e di effettuare il ragionamento inverso per vedere finalmente con certezza lo sforzo di ottimizzazione. Perché c'è un numero molto elevato di possibilità, ma una sola è quella ottimizzata! Logicamente, concluderà che questo oggetto è stato progettato e prodotto da persone intelligenti.
Quindi, se consideriamo che l'oggetto è artificiale e progettato con intelligenza, è forse possibile trovare una “traccia di ottimizzazione” nella sua geometria e nelle sue dimensioni, proprio come il nostro archeologo è riuscito a trovare una traccia di ottimizzazione nella forma della nostra lattina... Viceversa, se non troviamo nulla di conclusivo, il mistero rimarrà irrisolto...
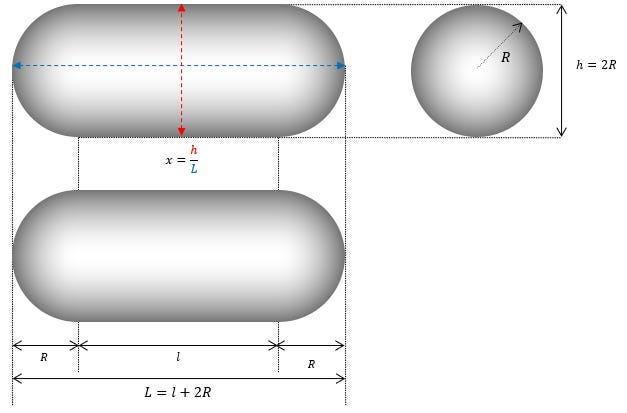
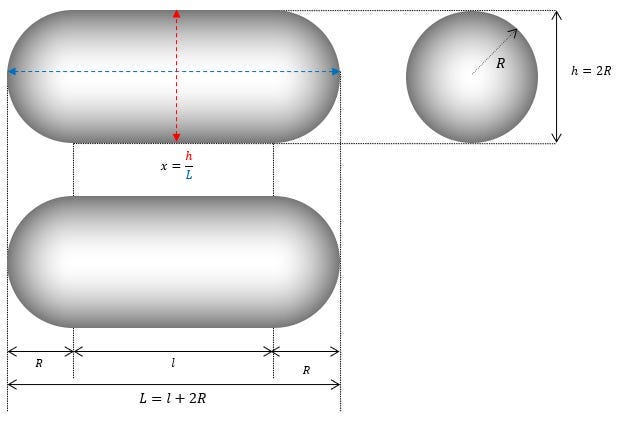
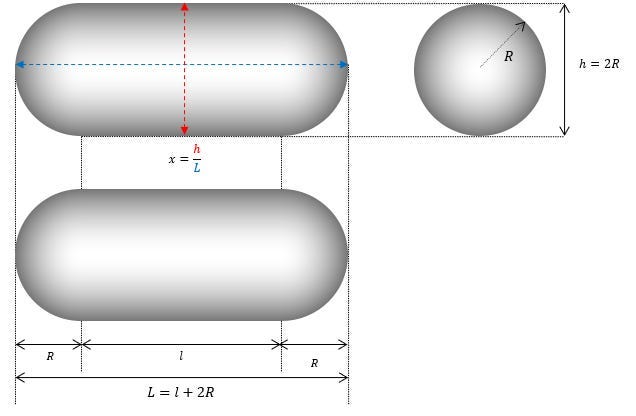
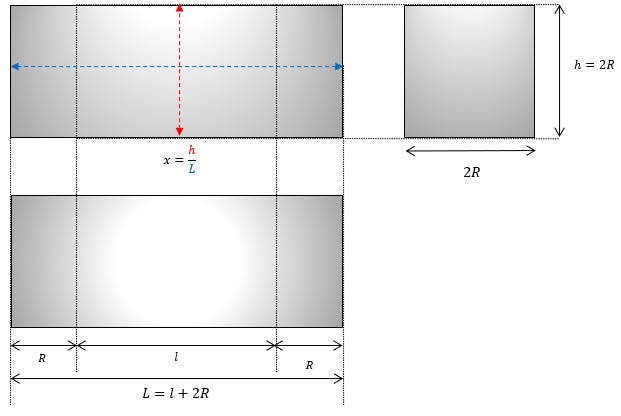
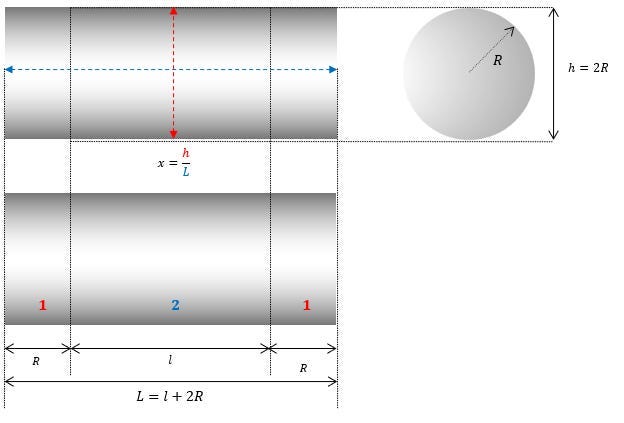
Per cominciare, notiamo che la forma di un TAC TIC richiede solo due parametri (R e x) per definire tutte le soluzioni possibili:
A questo punto possiamo notare che la geometria dell’oggetto comprende due tipi di superfici distinte:
Questa osservazione può sembrare banale, ma si rivelerà essenziale in seguito.
Una superficie cilindrica (il lato del cilindro appare in blu)
Due superfici sferiche (le semisfere alle estremità in rosso)
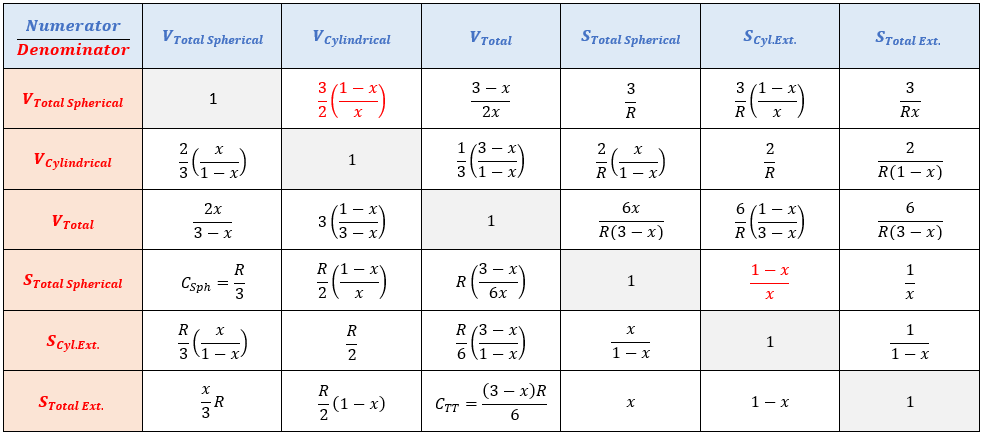
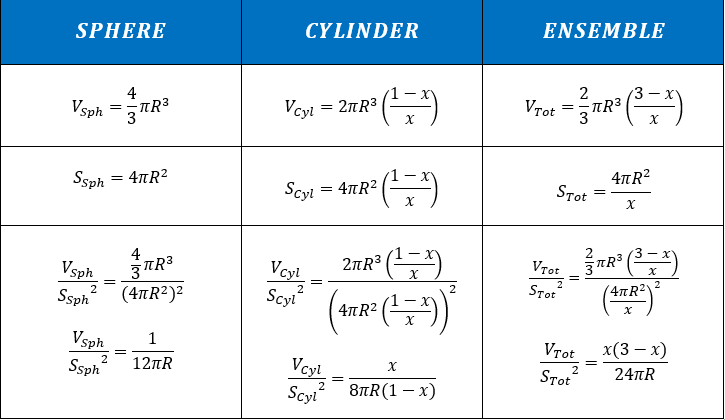
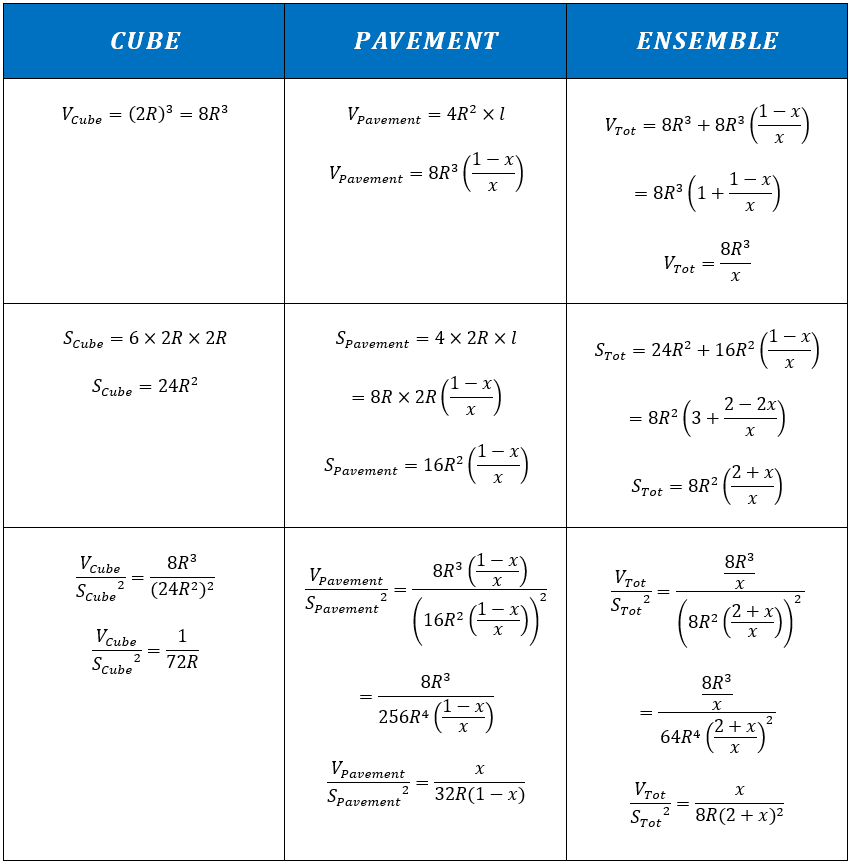
Descriviamo ora matematicamente i volumi e le superfici di ciascuna di queste parti e confrontiamoli tra loro mediante una matrice (i dettagli dei calcoli sono disponibili nell'allegato 2):
Da questo sviluppo non emerge nulla di particolare. Infatti, quando R e x sono indeterminati, non sembra emergere chiaramente alcuna relazione conclusiva.
Tentiamo ora lo stesso approccio introducendo uno dei due valori R o x. Non è possibile fornire una stima di R che sia sufficientemente precisa, d'altra parte, sulla base delle immagini visibili del video FLIR 1, è possibile fornire un quadro per x :
Le immagini dello spettro visibile sono più precise di quelle dello spettro IR, che tendono a “sfocare”.
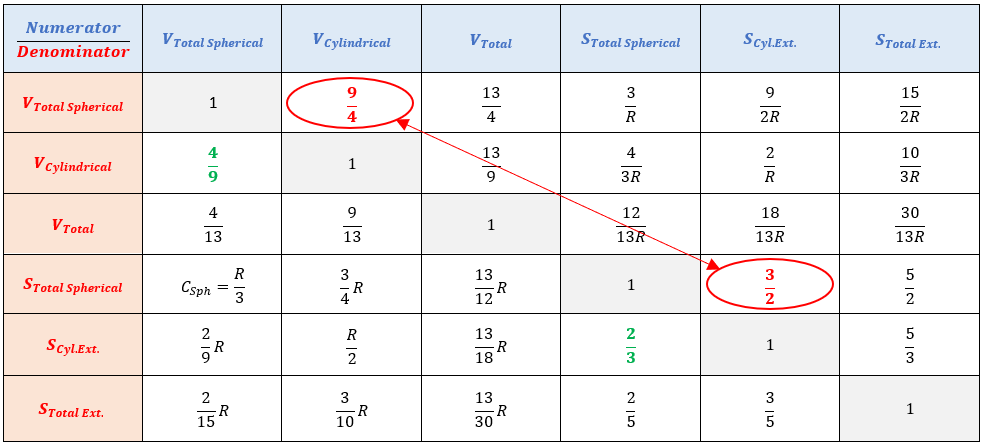
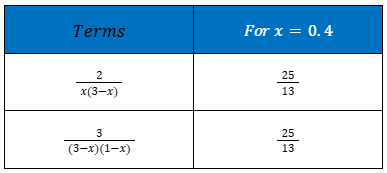
Torniamo quindi alla nostra tabella precedente con x=0,4 :
Per il valore di x=0,4, la matrice di confronto rivela ora una relazione singolare che lega i volumi e le superfici delle parti:
Che può anche essere scritta nella forma più elegante:
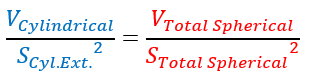
Per comodità, nel prosieguo dello studio questa relazione sarà indicata come V/S².
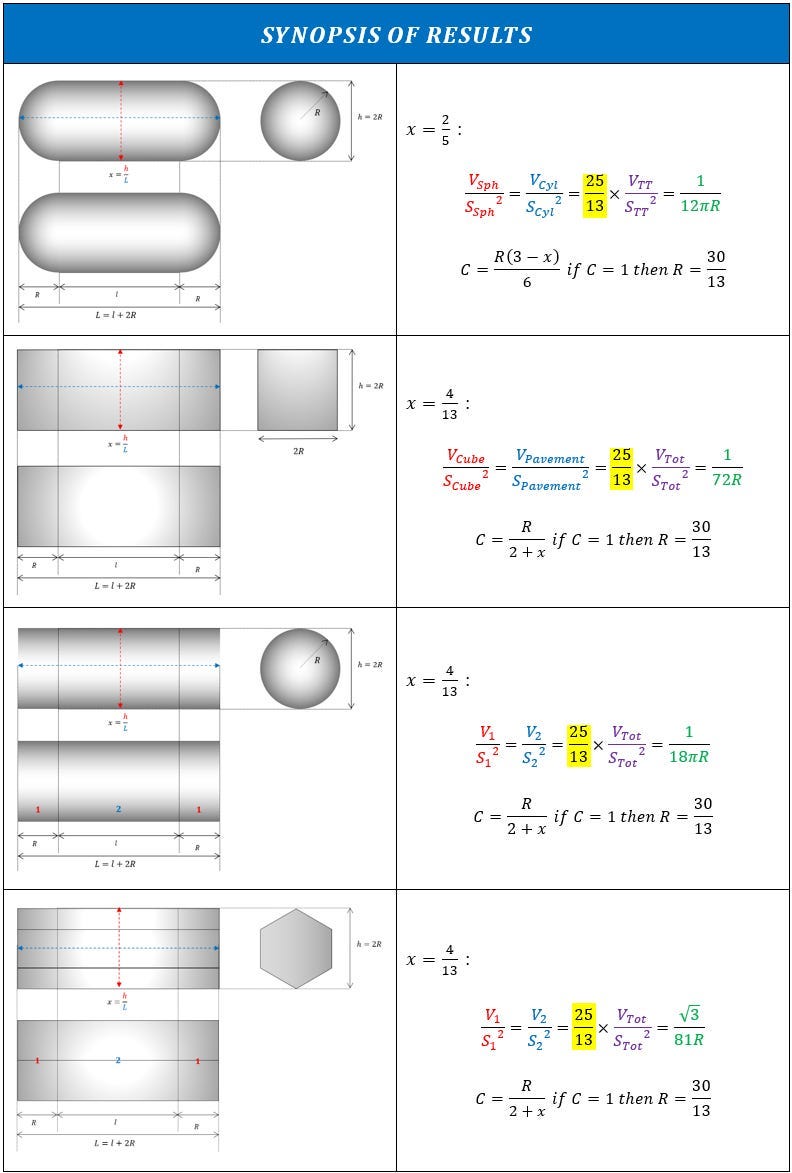
A questo punto, si può solo affermare che la forma osservata presenta effettivamente una relazione geometrica singolare, che compare solo per il rapporto altezza-lunghezza osservato, cioè per x=0,4 (Verifica disponibile nell'Allegato 3) :
La risoluzione del rapporto V/S² porta a una soluzione particolare per x che corrisponde esattamente al valore osservato sul video.
È quindi molto improbabile che questa particolare soluzione appaia per caso.
Questa osservazione tende a dimostrare che l'oggetto è effettivamente il frutto di un progetto ingegnoso la cui natura potrebbe essere legata alla relazione V/S². Se così fosse, questa relazione sarebbe quindi anche il punto di partenza per la progettazione della fusoliera.
Vedremo in seguito che questa relazione è in realtà la conseguenza di una relazione più generale, che esclude di fatto la possibilità di una coincidenza. Tuttavia, parlarne qui renderebbe il ragionamento anacronistico.
Potrebbe trattarsi di una coincidenza fortunata?
Per quanto debole, la possibilità di una coincidenza deve essere presa in considerazione, ma il cappio si stringe nuovamente quando studiamo l'aspetto della compattezza:
La compattezza è definita dal rapporto tra il volume di un oggetto e la sua superficie. Essa permette di confrontare la capacità delle forme geometriche di racchiudere il massimo volume in una superficie minima.
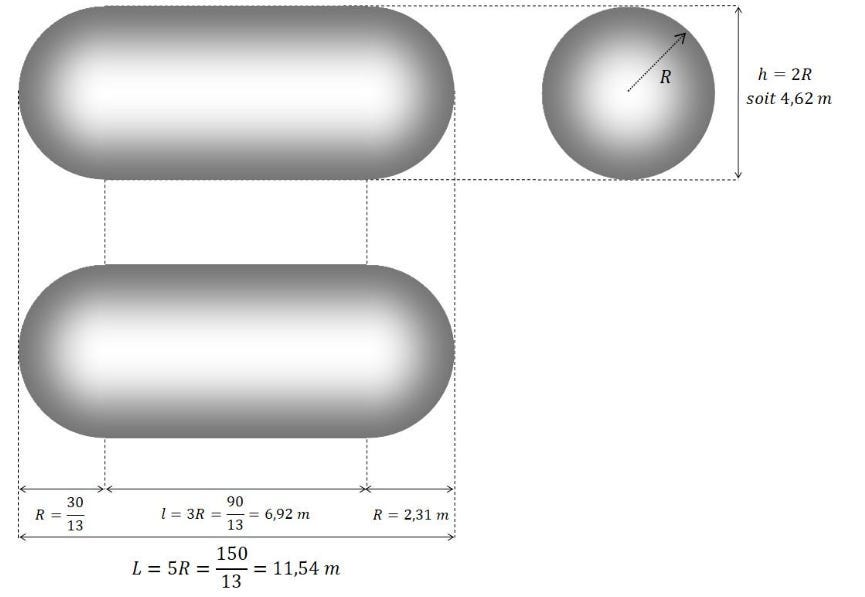
Per esempio, la sfera è la forma più efficiente con una compattezza di :
Determiniamo la compattezza della forma TIC TAC :
Che, per x=2/5 , diventa :
Ci manca ora una stima di R per dare un valore approssimativo di CTT.
Ricordiamo che i piloti hanno stimato la lunghezza del TIC TAC in circa 40 piedi (o circa 12 metri).
Ricordiamo anche la definizione di L sul diagramma: L=l+2R
Che per x=2/5 diventa :
Possiamo quindi fornire una stima della compattezza del TIC TAC:
Questo risultato non ci dà alcuna certezza e permette solo speculazioni difficilmente verificabili, ma che comunque meritano di essere presentate.
La stima della lunghezza di 40 piedi fornita dal pilota contiene ovviamente un'incertezza, a cui si aggiunge quella della conversione da piedi a metri. Possiamo quindi ragionevolmente chiederci se la compattezza reale non sia pari a 1.
Se consideriamo che :
Allora :
La lunghezza sarebbe quindi :
Che corrisponderebbe approssimativamente a 38 ft e risulterebbe compatibile con l'osservazione fatta dai piloti. Sulla base di questa ipotesi, possiamo quindi completare il diagramma iniziale e rischiare di dare una previsione approssimativa delle dimensioni del fenomeno:
È ovviamente sorprendente notare che due ragionamenti distinti possono portare a previsioni concordanti, sia per quanto riguarda il video (valore di x=0,4) sia per la stima della lunghezza dei piloti (11,54 m contro 12,19 m)
Questa concordanza è, di per sé, davvero sconcertante e tende a priori a favore di una progettazione oculata.
A tutti i fini pratici, i valori numerici degli altri aspetti geometrici sono riassunti di seguito:
Questo conclude la prima parte.
La seconda parte si rivela più difficile da spiegare e molto più matematica, ma è anche quella che, a mio parere, è la più convincente e la più sorprendente.
Cosa possiamo imparare dalla relazione V/S²?
Ricordiamo la relazione :
In questa forma non possiamo imparare molto di più. Dobbiamo introdurre un nuovo aspetto come l'espressione del volume e della superficie dell'insieme. L'idea è semplice e il risultato è molto facile da dimostrare (dimostrazione disponibile nell'allegato 4):
Otteniamo quindi questa tripla relazione che ci insegna che da un punto di vista geometrico l'insieme della forma è anche in relazione con le diverse parti. Ovviamente, i vincoli sono ancora più specifici di quanto immaginato in precedenza.
Inoltre, si nota il coefficiente 25/13... che, a mia conoscenza, non corrisponde ad alcuna costante in fisica. Nonostante le mie ricerche nella letteratura e nei fogli di calcolo ingegneristici, non riesco a trovare alcuna corrispondenza sia per la relazione che per il coefficiente 25/13.
La relazione permette comunque di “immaginare” un flusso (forse di natura elettromagnetica) scambiato tra i diversi volumi attraverso le diverse pareti, ma questa è un'interpretazione personale puramente speculativa. La motivazione di questa relazione potrebbe anche essere estetica, dopotutto.
Se, come per me, il processo vi sembra interessante fino a questo punto, è qui che diventa davvero confuso! Vi lascio giudicare da soli:
Vi risparmio i dettagli personali che mi hanno portato a questa idea e vi porto direttamente ai risultati:
Dopo innumerevoli tentativi di saperne di più, ho considerato la possibilità che la relazione non fosse unica per il TIC TAC. Ho quindi applicato la relazione ad altre forme “geometricamente vicine”. Vi lascio giudicare i risultati:
(I dettagli dei calcoli per ogni forma sono disponibili nell'allegato 5)
Applicando la relazione a forme diverse, otteniamo valori diversi per x ma troviamo sempre lo stesso coefficiente 25/13 ! Sembra quindi che quella che inizialmente consideravamo una relazione specifica per una singola forma geometrica sia, in realtà, un principio applicabile a diverse forme.
Per comodità, mi sono permesso di chiamarlo “Principio di Affinità Geometrica” o PAG, in riferimento a una terza parte incompiuta.
Ad oggi, sto considerando la possibilità che questo principio permetta di classificare le forme in base alle loro simmetrie. Forse sarebbe possibile classificare la famiglia 25/13 o altre famiglie ancora da scoprire. L'origine di questo principio potrebbe anche derivare da una conseguenza dei gruppi LIE o addirittura dall'applicazione di una lagrangiana a una relazione ancora indeterminata.
Comunque sia, il Principio di Affinità Geometrica è un oggetto matematico puro e indipendente dal fenomeno che ci mette sulle sue tracce. È un problema matematico a sé stante e deve essere affrontato, esplorato e analizzato come tale. La forma del TIC TAC sarebbe a priori solo un'applicazione del Principio di Affinità Geometrica. Interessarsi al solo caso del TIC TAC può quindi essere paragonato all'osservazione di un solo lato di un dado di cui ancora non conosciamo le reali dimensioni.
Resta comunque sorprendente e persino sconvolgente che la semplice curiosità matematica applicata a un caso di UAP abbia potuto portare a una tale scoperta...
Ci siamo chiesti quale fosse la natura del vantaggio che avrebbe potuto prevalere sull'aerodinamica. Dato che questo lavoro non ha finora portato alla luce alcuna costante della fisica e che la letteratura non fa alcun cenno alla relazione, non siamo in grado di collegare la nostra relazione ad alcuna necessità fisica o tecnica.
Nonostante i notevoli progressi, questo aspetto rimane un enigma.
Allegato 1 : Calcolo
Allegato 2 : Volumi e superfici di ogni parte e dell'insieme
Allegato 3 : Verifiche della relazione V/S²
Per il valore di x=0,4 e solo per questo valore, la tabella di confronto rivela una relazione notevole specifica della geometria del TIC-TAC:
Tornando alla prima tabella (prima che il valore di x=0,4 non fosse preso in considerazione) possiamo stabilire l'equazione iniziale:
Si noti che questa relazione è indipendente da R e dipende solo da x.
Quali sono le soluzioni di questa relazione? Espandendo otteniamo :
Allora
che dà l'equazione quadratica :
Quindi per la forma
il cui discriminante si scrive :
deduciamo le radici :
Troviamo quindi x=0,4 in perfetto accordo con le osservazioni del video FLIR1.
Soluzione sferica (corrisponde a una soluzione in cui l=0)
La risoluzione della relazione V/S² porta a una soluzione particolare per x che corrisponde esattamente al valore osservato sul video. È quindi molto improbabile che questa soluzione particolare appaia per caso.
Allegato 4: Estensione del rapporto V/S²
Calcoliamo i rapporti indicati nella prima colonna prima di esprimerli in base alla superficie o al volume della TIC TAC nella seconda colonna:
Utilizzando queste nuove espressioni e promemoria, esprimiamo i termini della relazione V/S2 in funzione di STT e VTT:
Applicando la relazione V/S², otteniamo :
Verifichiamo per quale/i valore/i di x è valida l'uguaglianza tra il TERZO e il QUINTO termine risolvendo :
Troviamo concordemente il valore x=0,4 ; che avvalora le nostre ipotesi e deduzioni precedenti. Calcoliamo ora il valore dei termini :
È così dimostrato che per il particolare valore x=0,4 possiamo applicare la relazione :
Si noti che questa formulazione non presuppone affatto il valore di R.
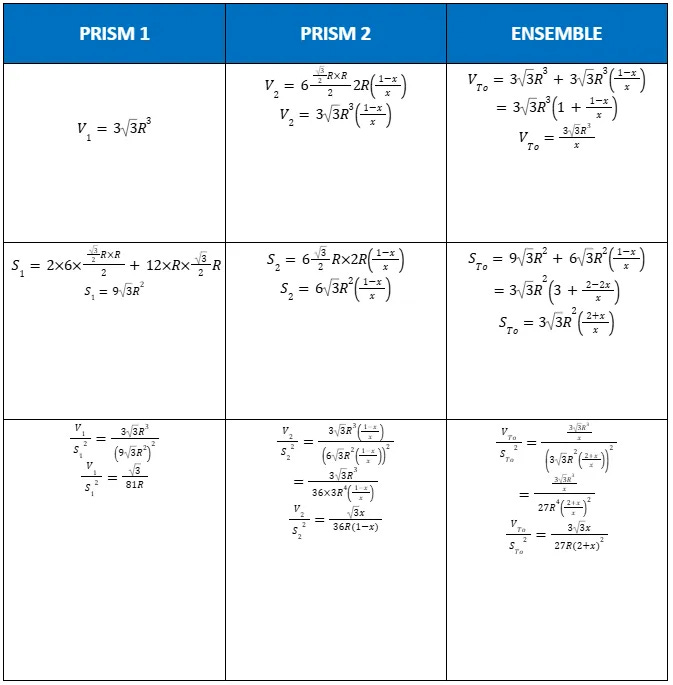
Allegato 5: Calcoli applicativi del principio di affinità geometrica a forme diverse
Ricordiamo la schematizzazione del fenomeno:
Ricordiamo l'espressione di l :
Nella prima parte, abbiamo evidenziato il particolare valore x :
L'uguaglianza dell'affinità geometrica tra le parti è quindi soggetta alla condizione x=2/5.
Confrontiamo ora l'affinità geometrica dell'insieme con quella di ciascuna parte:
Concludiamo che per la forma del Tic-Tac, la relazione di affinità geometrica si scrive :
PRISMA A SEZIONE QUADRATA
Come nel caso del TIC-TAC, si considera solo la superficie rivolta verso l'esterno.
Per quale valore di x possiamo osservare l'uguaglianza delle affinità geometriche tra le parti :
Confrontiamo le affinità geometriche dell'insieme con quelle di ciascuna parte:
In modo assolutamente sorprendente, troviamo quindi il rapporto di affinità geometrica con lo stesso fattore 25/13 :
Il rapporto 25/13 corrisponderebbe a una costante verso cui convergono le affinità geometriche in determinate condizioni?
A tutti i fini pratici, si aggiungono alcune osservazioni interessanti:
Calcoliamo la compattezza :
Per x=4/13 :
Ne consegue che se la compattezza è 1 allora R vale 30/13 esattamente come nel caso del TIC-TAC...
È molto sorprendente trovare così tanti risultati comuni tra due forme molto diverse.
Si noti anche che :
CILINDRO
La forma ricorda alcuni casi di UAP a forma di “sigaro”.
Schematizzate la forma in questo modo:
Come nel caso del TIC-TAC, si prende in considerazione solo la superficie rivolta verso l'esterno.
Per quale valore di x possiamo osservare l'uguaglianza delle affinità geometriche delle parti:
Confrontiamo le affinità geometriche dell'insieme con quelle di ciascuna parte:
In modo altrettanto sorprendente, troviamo ancora una volta la relazione di affinità geometrica con lo stesso fattore 25/13 :
A tutti i fini pratici, si aggiungono alcune osservazioni interessanti:
Calcoliamo la compattezza:
Poiché anche in questo caso x=4/13 :
Allo stesso modo se C=1 quindi R=30/13 ancora una volta esattamente come nel caso del TIC-TAC.
Sorprendentemente, si scopre che la compattezza del cilindro è esattamente la stessa del precedente lastricato a sezione quadrata.
PRISMA A SEZIONE ESAGONALE
Schematizziamo la forma in questo modo:
Come nei casi precedenti, si prende in considerazione solo la superficie rivolta verso l'esterno.
In queste condizioni, il raggio interno dell'esagono vale :
Per quale valore di x possiamo osservare l'uguaglianza delle affinità geometriche delle parti:
Confrontiamo le affinità geometriche dell'insieme con quelle di ciascuna parte:
Sempre con lo stesso stupore, troviamo ancora una volta il rapporto di affinità geometrica con lo stesso fattore 25/13 :
Solo l'ultimo termine sembra suggerire una variazione a seconda della forma geometrica.
È molto sorprendente notare il successo della relazione di affinità geometrica in questi pochi test.
A tutti i fini pratici, si aggiungono alcune osservazioni interessanti:
Calcoliamo la compattezza :
Poiché anche in questo caso x=4/13 :
Allo stesso modo se C=1 quindi R=30/13 ancora una volta esattamente come nel caso del TIC-TAC.
Sorprendentemente, si scopre che la compattezza del prisma esagonale è esattamente la stessa del blocco quadrato e del triplo cilindro.
Revisione della traduzione dall’inglese di Piero Zanaboni